Rootable의 개발일기
퀵 정렬(Quick Sort) 본문
📌 퀵 정렬이란
하나의 리스트를 피벗(pivot)을 기준으로 하나는 pivot보다 작은 값들의 부분리스트, 하나는 pivot보다 큰 값들의 부분리스트로 정렬한 뒤, 각 부분리스트에 대해 재귀적으로 정렬하는 방법
🚩 분할 정복(Divide and Conquer) 알고리즘
퀵 정렬은 기본적으로 '분할 정복' 알고리즘을 기반으로 정렬되는 방식이다. 다만, 병합 정렬(Merge Sort)과 다른 점은 병합 정렬은 하나의 리스트를 '절반' 으로 나누어 분할 정복을 하고, 퀵 정렬은 피벗(pivot)을 기준으로 분할 정복을 하기 때문에 하나의 리스트에 대해 비균등하게 나뉠 수 있다는 점이다.
일반적인 성능: 퀵 정렬 > 병합 정렬
퀵 정렬은 '비교 정렬' 이며, 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않으므로 '제자리 정렬(in-place sort)' 이라고도 한다. 또한, 두 개의 부분 리스트를 만들 때 서로 떨어진 원소끼리 교환이 일어나므로 '불안정정렬(Unstable Sort)' 알고리즘이기도 하다.
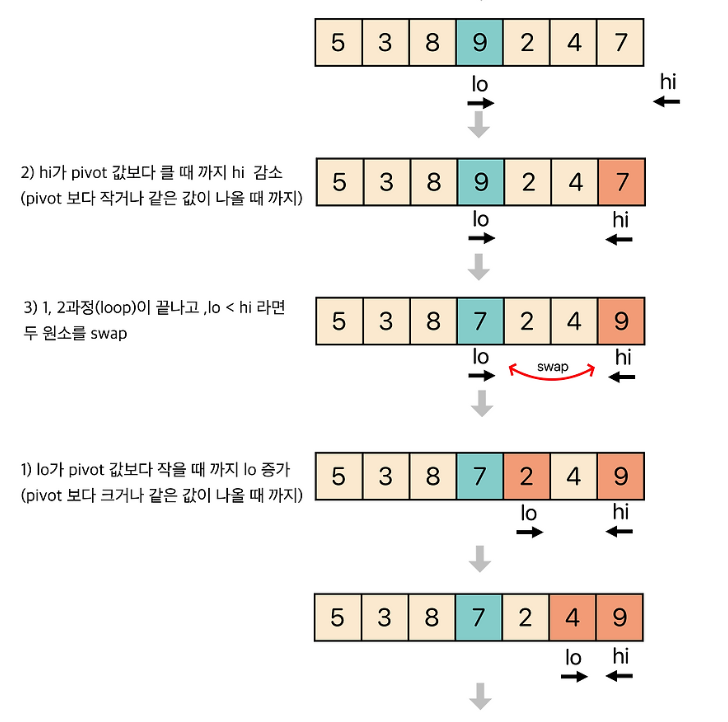
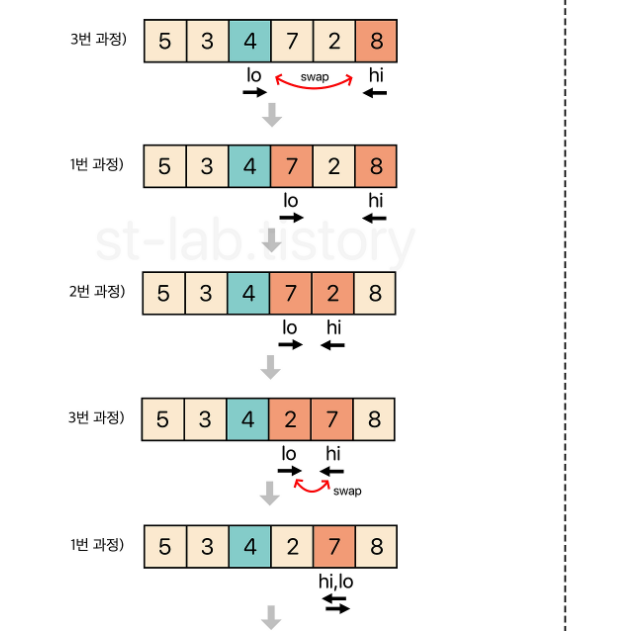
📌 정렬 과정
- 피벗 선택
- 피벗을 기준으로 왼쪽은 피벗보다 큰 값, 오른쪽은 피벗보다 작은 값을 탐색
- 양 방향에서 찾은 두 원소를 교환
- 왼쪽에서 탐색하는 위치와 오른쪽에서 탐색하는 위치가 엇갈리지 않을 때까지 2번으로 돌아가 위 과정을 반복
- 엇갈린 기점을 기준으로 두 개의 부분 리스트로 나누어 1번으로 돌아가 해당 부분 리스트의 길이가 1이 아닐 때까지 1번 과정을 반복(Divide: 분할)
- 인접한 부분리스틑끼리 병합 (Conqure: 정복)
🔍 왼쪽 피벗 선택 방식 (Lomuto 방식)
public class QuickSort {
public static void sort(int[] A) {
l_pivot_sort(A, 0, A.length - 1);
}
public static void l_pivot_sort(int[] A, int lo, int hi) {
if (lo >= hi) return;
int pivot = partition(A, lo, hi);
l_pivot_sort(A, lo, pivot - 1); //왼쪽 부분 리스트 정복
l_pivot_sort(A, pivot + 1, hi); //오른쪽 부분 리스트 정복
}
public static int partition(int[] A, int left, int right) {
int lo = left;
int hi = right;
int pivot = A[left];
while (lo < hi) {
while (A[hi] > pivot && lo < hi) hi--; //우측부터 pivot 보다 작은 값 찾기
while (A[lo] <= pivot && lo < hi) lo++; //좌측부터 pivot 보다 큰 값 찾기
swap(A, lo, hi);
}
swap(A, left, lo);
return lo;
}
public static void swap(int[] A, int i, int j) {
int tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
}
🔍 오른쪽 피벗 선택 방식 (Lomuto 방식)
public class QuickSort {
public static void sort(int[] A) {
r_pivot_sort(A, 0, A.length - 1);
}
public static void r_pivot_sort(int[] A, int lo, int hi) {
if (lo >= hi) return;
int pivot = partition(A, lo, hi);
r_pivot_sort(A, lo, pivot - 1); //왼쪽 부분 리스트 정복
r_pivot_sort(A, pivot + 1, hi); //오른쪽 부분 리스트 정복
}
public static int partition(int[] A, int left, int right) {
int lo = left;
int hi = right;
int pivot = A[right];
while (lo < hi) {
while (A[lo] < pivot && lo < hi) lo++; //좌측부터 pivot 보다 큰 값 찾기
while (A[hi] >= pivot && lo < hi) hi--; //우측부터 pivot 보다 작은 값 찾기
swap(A, lo, hi);
}
swap(A, right, hi);
return hi;
}
public static void swap(int[] A, int i, int j) {
int tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
}
🔍 중간 피벗 선택 방식 (Hoare 방식)
이미 피벗 기준으로 양쪽이 분할돼 있으므로, 피벗을 다시 옮길 필요 없다.
➡ 마지막에 pivot을 swap하지 않으므로, 두 포인터가 같아질 때 바로 swap 후 종료
public class QuickSort {
public static void sort(int[] A) {
m_pivot_sort(A, 0, A.length - 1);
}
public static void m_pivot_sort(int[] A, int lo, int hi) {
if (lo >= hi) return;
int pivot = partition(A, lo, hi);
m_pivot_sort(A, lo, pivot - 1); //왼쪽 부분 리스트 정복
m_pivot_sort(A, pivot + 1, hi); //오른쪽 부분 리스트 정복
}
public static int partition(int[] A, int left, int right) {
int lo = left;
int hi = right;
int pivot = A[(left + right) / 2];
while (lo <= hi) {
while (A[lo] < pivot) lo++;
while (A[hi] > pivot) hi--;
if (lo <= hi) {
swap(A, lo, hi);
lo++;
hi--;
}
}
return hi;
}
public static void swap(int[] A, int i, int j) {
int tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
}
📌 시간 복잡도
O(NlogN)의 시간복잡도

이상적으로 피벗이 중앙에 위치되어 리스트를 절반으로 나눈다고 할 때, N개의 데이터가 있는 리스트를 1개까지 쪼개어 트리로 나타내게 되면 Binary Tree 형태로 나온다. 알고리즘에서 피벗을 잡고 큰 요소와 작은 요소를 각 끝단에서 시작하여 탐색하며 만족하지 못하는 경우 swap 한다. 이는 현재 리스트의 요소들을 탐색하기 때문에 O(N)이다.
좀 더 자세하게 말하자면 i번째 레벨에서 노드의 개수가 2^i개이고, 노드의 크기(=한 노드에 들어있는 원소의 개수)는 N/2^i개다. 이를 곱하면 한 레벨에서 비교 작업에 대한 시간복잡도는 O(2^i * N/2^i)이고 곧 O(N)이다. 그리고 O(N)의 비교 작업을 트리의 높이인 logN-1번 수행하므로 O(NlogN)의 시간복잡도를 갖는 것을 알 수 있다. 퀵 정렬은 정렬된 상태의 배열을 정렬하고자 할 때 최악의 성능을 보인다.
❓ 퀵 정렬이 빠른 이유
적은 오버헤드와 참조 지역성(캐시 효율성)
1. 상수 요인(Constant Factor) 이 작다. (적은 오버헤드)
빅오(Big-O) 표기법은 데이터의 양(N)이 커질 때의 성장률을 나타낼 뿐, 실제 연산 횟수에 곱해지는 상수는 무시한다. 퀵 정렬의 핵심 연산(inner loop)은 단순한 비교와 값 교환(swap)으로만 이루어져 있어 매우 가볍다.
- 퀵 정렬: while (arr[i] < pivot) 처럼 단순 비교만 반복
- 병합 정렬: 정렬된 두 배열을 합치기 위해 추가적인 메모리 공간을 할당하고, 데이터를 복사하는 과정에서 상대적으로 무거운 작업(오버 헤드)이 발생
즉, 같은 O(NlogN) 이라도 실제 기계가 실행하는 명령어의 수가 퀵 정렬이 훨씬 적기 때문에 더 빠르다.
2. 참조 지역성(Locality of Reference) 원리를 잘 활용한다. (캐시 효율성)
CPU는 메모리(RAM)에서 데이터를 가져올 때, 속도가 훨씬 빠른 캐시 메모리에 해당 데이터와 그 주변 데이터를 함께 저장한다. 그 후, 필요한 데이터가 캐시에 있으면(Cache Hit) 메모리까지 가지 않고 매우 빠르게 작업을 처리한다.
- 퀵 정렬: 배열의 특정 구간(파티션) 내에서 순차적으로 데이터를 접근하며 정렬 ➡ 한번 캐시에 올라온 데이터를 계속 활용할 가능성이 높아 캐시 히트율(Cache Hit Ratio)이 매우 높음
- 다른 정렬 방식: 데이터 접근이 상대적으로 여기저기 흩어져 있어 캐시 효율성이 떨어질 수 있음
"퀵 정렬은 한 페이지에 있는 글자들을 순서대로 읽는 것, 병합 정렬은 책의 10페이지와 100페이지를 번갈아 보는 것"
📌 Hoare vs Lomuto 비교
pivot의 처리 방식과 분할 효율성 차이
Lomuto 방식은 피봇을 정하고 그보다 작은 값을 왼쪽으로, 큰 값을 오른쪽으로 보내 피봇의 최종 위치를 정합니다. 이 방식은 직관적이지만, 이미 정렬된 배열 같은 특정 경우에 성능이 크게 저하될 수 있다.
반면, Hoare 방식은 배열 양 쪽 끝에서부터 탐색하여 피봇보다 크거나 작은 값을 교환해 나간다. 이 방식은 최종 위치가 정해지진 않지만, 일반적으로 Lomuto 방식보다 비교와 교환 횟수가 적어 더 빠르고 효율적이다.
📌 정리
🥦 평균적으로 매우 빠른 속도
시간 복잡도가 O(NlogN) 이다. 다른 O(NlogN) 정렬 알고리즘 대비 오버헤드가 적고 캐시 효율성(참조 지역성)이 높아 실제 실행 속도가 가장 빠른 정렬 알고리즘 중 하나다.
🥦 제자리 정렬(In-place sort)
정렬을 위한 별도의 추가 메모리가 필요하지 않음. 이는 대용량 데이터를 정렬할 때 큰 장점
🥦 최악의 경우 성능 저하(O(N^2))
pivot 이 한 쪽으로 치우치게 선택될 경우 (이미 정렬된 배열) 시간 복잡도가 O(N^2)으로 성능이 급격히 나빠질 수 있음
🥦 불안정 정렬(Unstable sort)
값이 같은 데이터들의 기존 순서가 정렬 후에도 유지되지 않을 수 있음. 따라서 데이터의 기존 순서가 중요한 경우에는 사용하기 부적합.
References:
https://st-lab.tistory.com/250
자바 [JAVA] - 퀵 정렬 (Quick Sort)
[정렬 알고리즘 모음] 더보기 1. 계수 정렬 (Counting Sort) 2. 선택 정렬 (Selection Sort) 3. 삽입 정렬 (Insertion Sort) 4. 거품 정렬 (Bubble Sort) 5. 셸 정렬 (Shell Sort) 6. 힙 정렬 (Heap Sort) 7. 합병(병합) 정렬 (Merge
st-lab.tistory.com
'알고리즘' 카테고리의 다른 글
| 허프만(Huffman) 알고리즘 (0) | 2024.05.29 |
|---|---|
| 냅색(Knapsack) 알고리즘 (0) | 2023.11.17 |
| 메모이제이션과 타뷸레이션 (0) | 2023.10.30 |
| 이진 탐색(Binary Search) (0) | 2023.10.29 |
| 삽입 정렬(Insertion Sort) (0) | 2023.10.26 |