유니온 파인드(union-find) 알고리즘
여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union 연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성된 알고리즘
📌 union, find 연산
- union 연산 : 각 노드가 속한 집합을 1개로 합치는 연산
- 노드 a, b가 a ∈ A, b ∈ B일 때 union(a, b) == A U B
- find 연산 : 특정 노드 a에 관해 a가 속한 집합의 대표 노드를 반환하는 연산
- 노드 a가 a ∈ A일 때 find(a)는 A 집합의 대표 노드를 반환
📌 원리
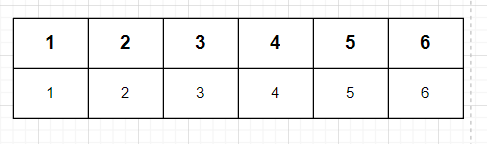
🔎 1차원 배열
1차원 배열을 통해 초기 배열을 생성한다. 초기 배열은 인덱스가 곧 값이 되며, 이는 각 노드가 속한 집합이 없어 자신이 대표 노드가 된 상태인 것이다.

🔎 union 연산
2개의 노드를 선택하여 대표 노드를 정하는 연산이다. 대표 노드를 정하는 방식에 정해진 룰은 없다. 여기서는 두 값 중 작은 값으로 정했다.
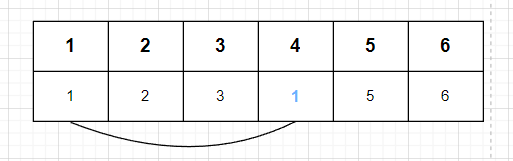


✔ 각 노드의 대표끼리 union 연산(⭐)
대표가 아닌 노드를 자식 노드라고 부른다. 두 노드의 union 연산은 대표 노드 사이의 union 연산이 되도록 해야 한다. 따라서, 자식 노드는 최상위 부모 노드를 찾아야 하며 해당 부모 노드 사이에 union 연산이 되도록 한다.
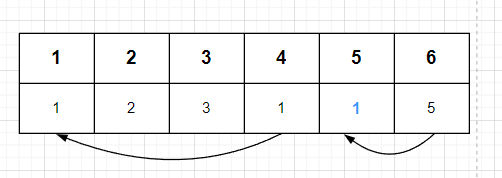
//집합 만들기
static void union(int a, int b) {
int pa = find(a); //a의 대표 노드
int pb = find(b); //b의 대표 노드
if (pa < pb) A[pb] = pa;
else A[pa] = pb;
}
union(4,6)을 수행할 때, 4와 6은 대표 노드가 아니다. 그래서 해당 인덱스의 값을 추적하여 부모 노드를 찾아야 한다. 각 부모 노드인 1과 5를 찾은 후 두 값 중에 작은 1을 부모 노드로 했다.
🔎 find 연산
자신이 속한 집합의 대표 노드를 찾는 연산이다. 이는 단순히 대표 노드를 찾는 역할만 하는 것이 아니라 그래프를 정돈하고 시간 복잡도를 개선한다.
✔ find 연산 작동 과정(⭐)
//A는 유니온 파인드 배열, a는 노드 인덱스
int find(int a) {
if (a == A[a]) return a;
else return A[a] = find(A[a]); //모든 자식 노드의 값을 대표 노드값으로 변경
}
재귀를 통해 자식의 부모 노드를 계속해서 추적한다. 추적 끝에 상위 노드가 존재하지 않는 최상위 노드를 만나면 재귀는 종료된다. 여기서 주의할 점은 탐색한 모든 자식 노드의 값을 대표 노드값으로 변경하는 부분이다. 이로써, 탐색 대상 노드들(자식 노드들)은 동일한 집합(부모)으로 묶이게 된다.


이렇게 연산을 할 때 거치는 노드들이 대표 노드와 바로 연결되는 형태가 되면 추후 노드와 관련된 find 연산 속도가 O(1)로 변경된다. 결국, 한 번의 find 연산으로 모든 노드가 루트 노드에 직접 연결되는 것이다. 이러한 형태로 변경되면 이후 find 연산이 진행될 때 경로 압축의 효과가 나타난다.
💡 경로 압축
실제 그래프에서 여러 노드를 거쳐야 하는 경로에서 그래프를 변형해 더 짧은 경로로 갈 수 있도록 함으로써 시간 복잡도를 효과적으로 줄이는 방법
Reference:
